We Are Living in the Midst of One of the Biggest Bond Bubbles in History
Today, I was sitting at the dining room table, drinking a cup of coffee wearing the Brooks Brothers pajamas I picked up on my birthday a few days ago, and watching the stock market skyrocket when it occurred to me that, given the project we are working on right now and some other things going on at the business, I want to build some cash and bond reserves at one of the individual operating companies; maybe put aside money a little at a time, let it build and do something fun with it three or four years from now, like design and build a row of townhouses or whatever.
 Honestly, I can’t explain it but it was a strong enough inclination that I called Aaron and had a conversation detailing my thought process and, a few minutes later, was on the phone selling off some Berkshire Hathaway, Campbell Soup Company, shares of a sugar refinery, and stock options that were held in the account of this particular business. Then, I set out to find a place to park the money. I wanted to take very little risk with the capital, avoid interest rate sensitivity (so virtually no bond duration), and high liquidity.
Honestly, I can’t explain it but it was a strong enough inclination that I called Aaron and had a conversation detailing my thought process and, a few minutes later, was on the phone selling off some Berkshire Hathaway, Campbell Soup Company, shares of a sugar refinery, and stock options that were held in the account of this particular business. Then, I set out to find a place to park the money. I wanted to take very little risk with the capital, avoid interest rate sensitivity (so virtually no bond duration), and high liquidity.
It took about three seconds to realize that interest rates really are effectively zero. Obviously I knew this. But I don’t think I truly grasped it since I’m a long way away from my fixed income days given how relatively young I am.
There is no way, short of massive deflation (which I think is unlikely) that bond prices aren’t going to suffer on a real inflation-adjusted net-of-tax basis at some point in the future because interest rates must rise (meaning bond values must fall) if there is even a modicum of inflation. It is just a function of the bond valuation model. There is no margin of safety built into the system at all at current levels, which means someone holding Treasury bonds, municipal bonds or corporate bonds with 20+ year maturities is going to get hit hard, perhaps experiencing double-digit drops in the market price of the bond. The real net purchasing power declines will be even more painful. The only exception would be a bond such as a savings bond, which can be sold back at par value any time the investor desires.
Ultimately, I bought a series of brokered certificates of deposit from an FDIC insured bank in the South that had a Tier 1 capital ratio of somewhere north of 33% (in the banking world, a Tier 1 of 8% or 9% is considered strong so this is Fort Knox-like). I figured until I knew exactly what I wanted to do, I’d tie the money up in a laddered maturity system with rolling maturities coming due every 30 days for the next few months.
A Look at Actual Bond Yields on the Market Today
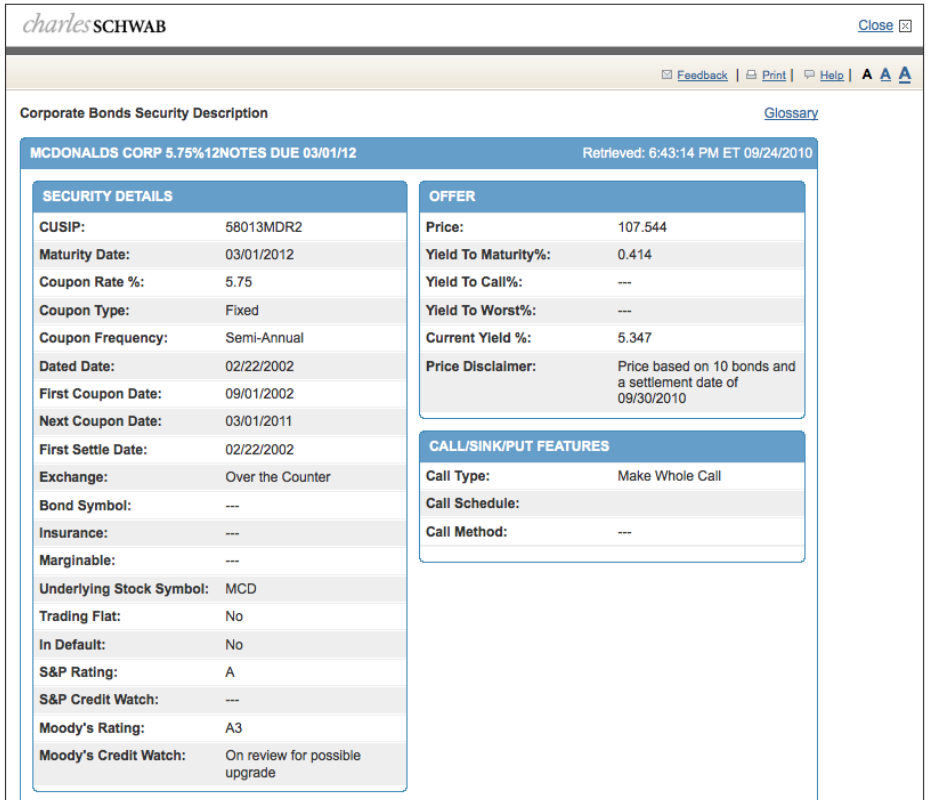
Here is one of the bond issues I considered today – McDonald’s Corporation 5.75% notes that mature in March 2012. The bonds had a face value of $1,000 and paid $57.50 in interest to the bond holder each year, divided semi-annually (so $28.75 every six months). To explain the bond valuation, I will run a scenario where we purchased ten bonds with a face value of $10,000.
The bonds mature in March of 2012, or roughly 17 months away. The last interest payment was made on September 1st so you have three payments of $28.75 per bond remaining remaining, or $287.50 for ten bonds. That is, you will receive the following interest income from the bonds:
- March 2011 = $28.75 interest income x 10 bonds = $287.50
- September 2011 = $28.75 interest income x 10 bonds = $287.50
- March 2012 = $28.75 interest income x 10 bonds = $287.50
- plus bond maturity = $1,000 for the par value of the bond, which is returned to you. The bond then ceases to exist. That means you’ll get the entire $10,000 back on this date.
Put simply, if you buy the ten McDonald’s corporate bonds today, your scheduled cash flows consist of $862.50 in interest income plus $10,000 returned to you for the par value of the bond 17 months from now. Your total cash flow generated will be $10,862.50 over that period.
The Bonds Don’t Trade at Par Value
When the McDonald’s bonds were issued in 2002, they were originally issued at $1,000 each and yielded 5.75%, or $57.50 every year. In the years since, interest rates have fallen. Investors saw the rich yield McDonald’s offered and bought the bonds, driving the price higher. As the price increased, the yield fell until it finally reached a level that was approximately the same as other corporate bonds issued today.
As a result, it would now cost you $10,800.72 to buy the ten McDonald’s bonds, not an even $10,000 (10 bonds x $1,000 each). Here is a look at the proposal sheet from one of the brokers:

In other words, you are going to buy the bonds today for $10,800.72 and then cash them in for $10,000 in 18 months. That is a loss of $800.72 on the par value of the bonds.
At the same time, you are scheduled to collect $862.50 in interest income during that time period. If you offset the interest income with the scheduled capital loss on the bonds, you are left with an estimated pre-tax profit of $61.78 [$862.50 interest income – $800.72 capital loss on par value of bond = $61.78].
What Is Your Yield to Maturity, or Compound Annual Growth Rate if You Buy the Bonds?
How much does that work out to on a compounded annual growth rate basis? What is your APY? That is easy. First you calculate your total gain:
$61.78 pre-tax gain ÷ $10,800.72 cost basis = 0.00572, which is 0.572%
Next, you raise the total gain to the X-Root, which is the total compounding period divided into 1. We were compounding for roughly 17 months, or 1.5833 years so we take 1 ÷ 1.5833 years = 0.63159. We can raise our total gain to this power to calculate our annual percentage yield.
(1+.00572) ^ 0.63159 = 1.0036088.
We drop the 1, and get 0.0036, which is the equivalent to 0.36% compounded
You can even check your math using the FV of a single sum formula:
PV(1+i)^n
$10,800.72 investment(1.0036)^1.588 years
= $10,800.72(1.005722847673468)
= $10,862.53
(Note, the 3 cent difference from the actual future value of the bond, $10,862.50, is due to rounding)
In other words, for tying up your money in McDonald’s corporate bonds today, you can expect to earn an APY of 0.36% on your money. That works out to a whopping $61.78 for every 10 bonds you buy. This factors in all the purchasing costs, so it is the “real” yield to maturity for the bonds, not the 0.414% that the broker shows.
Money Costs Nothing Now
This leads to the point that for all intents and purposes, from a macroeconomic point of view, I am convinced that money has reached an effective cost of zero. The problem is, not everyone can access money because no rational investor is willing to loan it out for 30 years. In fact, the 30 year bond rates are anemic at only 4% to 7% depending upon the issuer.
Only huge companies such as many of the blue chip enterprises that make up the Dow Jones Industrial Average and/or S&P 500 components can take advantage of the situation with one notable exception – real estate mortgages. Someone who is financially strong and can afford the risk of further declines in the market, in theory, could lock in 30-year rates on mortgages to build, develop and / or acquire properties such as apartment buildings and hotels. This would give them a massive funding advantage if and when rates rose down the line.
The other side of the coin, though, is that someone who has a high bond duration, or high interest rate sensitivity, is going to get royally screwed. I mean, devastating, horrific losses. If you own nothing but bonds that mature 20, 25, or 30+ years from now, when interest rates rise, you are going to get your financial ass(ets) handed to you on a platter because the bonds must, in a rational market, fall far enough below par to result in the yield-to-maturity matching other fixed income investments of comparable credit and liquidity quality.
Explaining the reasons, though, would make this article too long so I’ll write a new one focusing on the potential dangers of long-maturities in a bond portfolio at some point in the future.


